A vital aspect of human intelligence is the ability to compose increasingly complex concepts out of simpler ideas, enabling both rapid learning and adaptation of knowledge. In this paper we show that energy-based models can exhibit this ability by directly combining probability distributions. Samples from the combined distribution correspond to compositions of concepts. For example, given a distribution for smiling faces, and another for male faces, we can combine them to generate smiling male faces. This allows us to generate natural images that simultaneously satisfy conjunctions, disjunctions, and negations of concepts. We evaluate compositional generation abilities of our model on the CelebA dataset of natural faces and synthetic 3D scene images. We also demonstrate other unique advantages of our model, such as the ability to continually learn and incorporate new concepts, or infer compositions of concept properties underlying an image.

The Problem with Existing Concept Representations

Existing works on representing visual concepts can be divided into two separate categories. One category of approaches represent global factors of variation, such as facial expression, by situating them on a fixed underlying latent space, such as the β-VAE model. A separate category of approaches represent local factors of variation by a set of as segmentation masks, as exemplified by the MONET model. While the former can enable representing global concepts, and the latter local concepts, there does exist a concept representation that can represent both in an unified manner. In this paper, we propose instead to represent concepts as EBMs. Such an approach enables us to represent both global factors of variation as well as local object factors of variation. Furthermore, we show that our concept representation enables us to combine disjointly learned factors together in a zero shot manner.

Compositional Visual Generation with Energy Based Models

Energy based models (EBMs) represent a distribution over data by defining an energy \(E_\theta(x) \) so that the likelihood of the data is proportional to \( \propto e^{-E_\theta(x)}\). Sampling in EBMs is done through MCMC sampling, using Langevin dynamics. Our key insight in our work is that underlying probability distributions can be composed together to represent different composition of concepts. Sampling under the modified probability distributions may then be done using Langevin dynamics. We define three different composition operators over probability distributions, for the standard logical operators of conjunction, disjunction, and negation which we illustrate below.

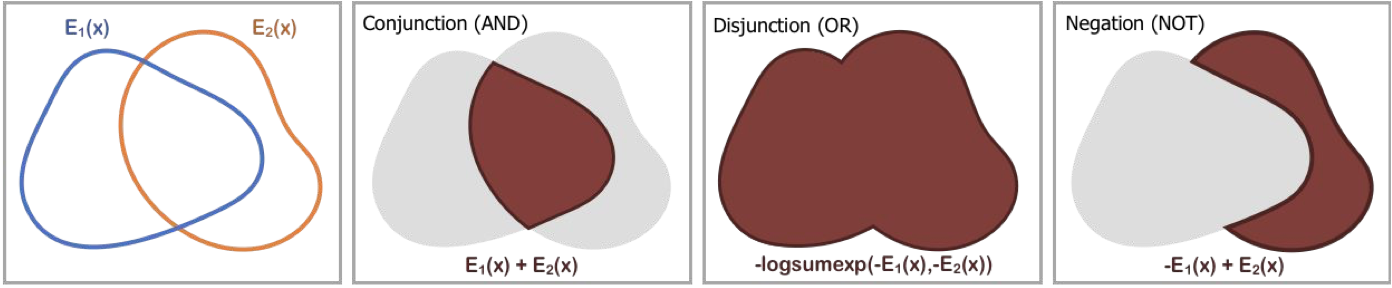
Conjunction

In concept conjunction, given separate independent concepts (such as a particular gender, hair style, or facial expression), we wish to construct an generation with the specified gender, hair style, and facial expression -- the combination of each concept. The likelihood of such an generation given a set of specific concepts is equal to the product of the likelihood of each individual concept \[ p(x|c_1 \; \text{and} \; c_2, \ldots, \; \text{and} \; c_i) = \prod_i p(x|c_i) \propto e^{-\sum_i E(x|c_i)}. \] We utilize Langevin sampling to sample from this modified EBM distribution.

Disjunction

In concept disjunction, given separate concepts such as the colors red and blue, we wish to construct an output that is either red or blue. We wish to construct a new distribution that has probability mass when any chosen concept is true. A natural choice of such a distribution is the sum of the likelihood of each concept: \[ p(x|c_1 \; \text{or} \; c_2, \ldots \; \text{or} \; c_i) \propto \sum_i p(x|c_i) / Z(c_i). \] where \( Z(c_i) \) denotes partition function for the chosen concept. We utilize Langevin sampling to sample from this modified EBM distribution.

Negation

In concept negation, we wish to generate an output that does not contain the concept. Given a color red, we want an output that is of a different color, such as blue. Thus, we want to construct a distribution that places high likelihood to data that is outside a given concept. One choice is a distribution inversely proportional to the concept. Importantly, negation must be defined with respect to another concept to be useful. The opposite of alive may be dead, but not inanimate. Negation without a data distribution is not integrable and leads to a generation of chaotic textures which, while satisfying absence of a concept, is not desirable. Thus in our experiments with negation we combine it with another concept to ground the negation and obtain an integrable distribution: \[ p(x| \text{not}(c_1), c_2) \propto \frac{p(x|c_2)}{p(x|c_1)^\alpha} \propto e^{ \alpha E(x|c_1) - E(x|c_2) } \] We utilize Langevin sampling to sample from this modified EBM distribution.

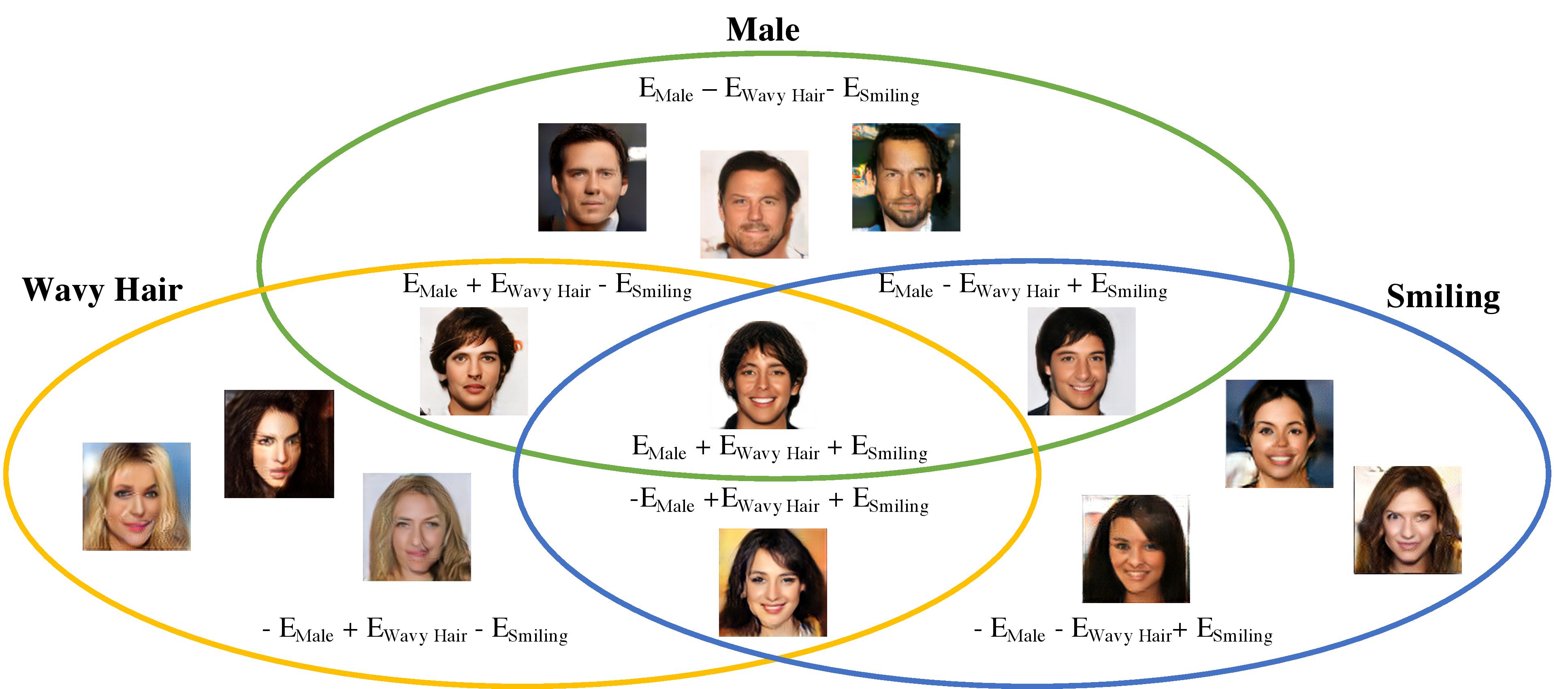
Concept Composition

Global Factor Compositional Generation

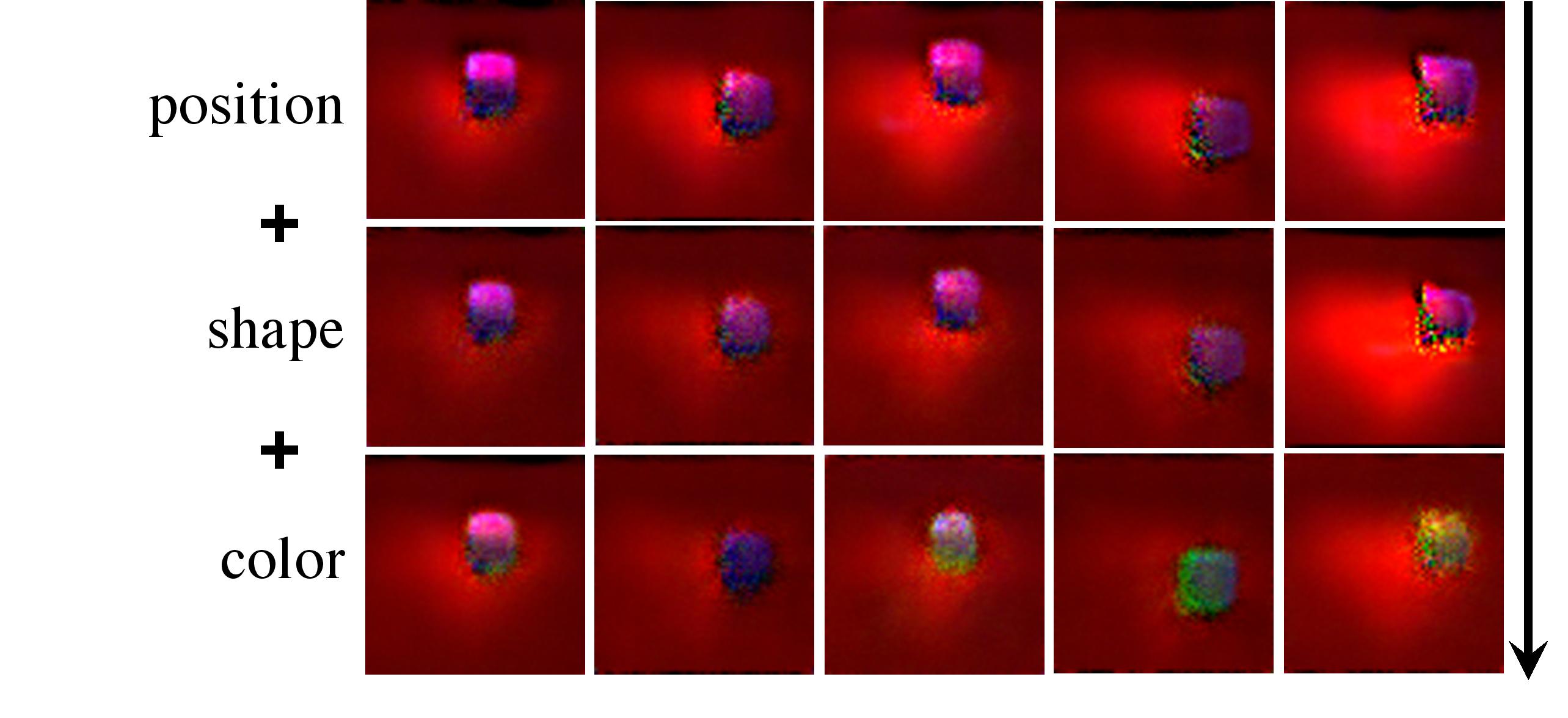
We first explore the ability of our models to compose different global factors of variation. We train seperate EBMs on the attributes of shape, position, size and color. Through conjunction on each model sequentially, we are able to generate successively more refined versions of an object scene.

We can similarily train seperate EBMs on the attributes of young, female, smiling, and wavy hair. Through conjunction on each model sequentially, we are able to generate successively more refined versions of human faces. Surprisingly, we find that generations of our model are able to become increasingly more refined by adding more models.

Higher Level Composition

We can further compose seperately trained EBMs in additional ways by nesting the compositional operators of conjunction, disjunction and negation. In the figure below, we showcase face generations of nested compositions.

Object Level Compositional Generation

We can also learn EBMs on the object attributes. We train a single EBM model to represent the position attribute. By summing EBMs conditioned on two different positions (conjunction), we can compositionally generate different number of cubes at the object level.

Continual Learning of Visual Concepts

By having the ability to compose in a zero-shot manner, EBMs enable us to learn, combine, and compose visual concepts acquired in a continual manner. To test this we consider:

• A dataset consisting of position annotations of purple cubes at different positions.
• A dataset consisting of shape annotations of different purple shapes at different positions.
• A dataset consisting of color annotations of different color shapes at different positions.

Related Projects

Check out our related projects on utilizing energy based models!

Energy-Based Models for Continual Learning

We show how EBMs help provide an orthogonal approach towards tackling continual learning problems by changing the underlying training objective to causes less interference with previously learned information. Our proposed EBM formulation is simple, efficient, and outperforms baseline methods by a large margin on several benchmarks. We further show that EBMs are adaptable to a harder continual learning setting where the data distribution changes without explicitly delineated task boundaries.

Energy Based Models for Atomic Level Protein Conformations

We introduce EBMs for modeling the underlying energy landscape of atomic level protein conformations. We train EBMs to predict the energy of different protein rotamer configurations, and find that our trained EBM models can nearly match the performance of classical energy function Rosetta on the task of protein sidechain prediction.

Model Based Planning with Energy Based Models

We present a framework towards utilizing EBMs to learn, in an online fashion, trajectory level plans for different start and goal configurations. This allows us to flexibly change and adapt to different sets of goals by changing the underlying trajectory inference objective.

Paper

---