Inferring Relational Potentials in Interacting Systems
Abstract
Systems consisting of interacting agents are prevalent in the world, ranging from dynamical systems in physics to complex biological networks. To build systems which can interact robustly in the real world, it is thus important to be able to infer the precise interactions governing such systems. Existing approaches typically discover such interactions by explicitly modeling the feed-forward dynamics of the trajectories. In this work, we propose Neural Interaction Inference with Potentials (NIIP) as an alternative approach to discover such interactions that enables greater flexibility in trajectory modeling: it discovers a set of relational potentials, represented as energy functions, which when minimized reconstruct the original trajectory. NIIP assigns low energy to the subs et of trajectories which respect the relational constraints observed. We illustrate that with these representations NIIP displays unique capabilities in test-time. First, it allows trajectory manipulation, such as interchanging interaction types across separately trained models, as well as trajectory forecasting. Additionally, it allows adding external hand-crafted potentials at test-time. Finally, NIIP enables the detection of out-of-distribution samples and anomalies without explicit training.
Method
Neural Interaction Inference with Potentials. We present Neural Interaction Inference with Potentials (NIIP), our unsupervised approach to decompose a trajectory $ \mathbf{x}(1...T)_i $, consisting of $ N $ separate nodes at each timestep, into a set of separate EBM $ E_\theta^j(\mathbf{x}) $ potentials. NIIP is composed by two steps: (i) an encoder for obtaining a set of potentials and (ii) a sampling process which optimizes for a predicted trajectory, minimizing the inferred potentials. Energy functions in NIIP are trained using autoencoding.
Relational Potentials. To effectively parameterize different potentials for separate interactions, we learn a latent conditioned energy function $ E_\theta(\mathbf{x}, \mathbf{z}) : \mathbb{R}^{T \times D} \times \mathbb{R}^{D_z} \xrightarrow{} \mathbb{R}$. Then, inferring a set of different potentials corresponds to inferring a latent $ \mathbf{z} \in \mathbb{R}^{D_z} $ that conditions an energy function. Given a trajectory $ \mathbf{x}(1...T)_i $, we infer a set of $ L $ different latent vectors for each directed pair of interacting nodes in a trajectory. Thus, given a set of $ N $ different nodes, this corresponds to a set of $ N(N-1)L $ energy functions.
To generate a trajectory, we optimize the energy function $ E(\mathbf{x}) = \sum_{ij,l} E_\theta^{ij,l}(\mathbf{x};\mathbf{z}_{ij,l}) $, across node indices $ i $ and $ j $ from $ 1 $ to $ N $ and latent vectors $ l $ from $ 1 $ to $L $. However, assigning one energy function to each latent code becomes prohibitively expensive as the number of nodes in a trajectory increases. Thus, to reduce this computational burden, we parameterize $L $ energy functions as shared message passing graph networks, grouping all edge contributions $ ij $ in a single network.
Inferring Energy Potentials. We utilize $ \text{Enc}_{\theta}(\mathbf{x}): \mathbb{R}^{T \times D} \xrightarrow{} \mathbb{R}^{D_z} $ to encode the observed trajectories $ \mathbf{x} $ into $ L $ latent representations per edge in the observation. We utilize a fully connected GNN with message-passing to infer latents. Instead of classifying edge types and using them as a gate ouputs, we utilize a continuous latent code $ \mathbf{z}_{ij,l} $, allowing for higher flexibility.
Training Objective. To train NIIP, we infer a set of different EBM potentials by auto-encoding the underlying trajectory. In particular, given a trajectory $ \mathbf{x}(1...T)_i=\left(\mathbf{x}(1)_i,\dots,\mathbf{x}(T)_i\right) $, we split the trajectory into initial conditions $ \mathbf{x}(1...T_0) $, corresponding to the first $ T_0 $ states of the trajectory and $ \mathbf{x}(T_0...T) $, corresponding to the subsequent states of the trajectory, where each state of the trajectory consists of $ N $ different nodes. The edge potentials are encoded by observing a portion of the overall trajectory $ \mathbf{x}(1...T^\prime) $, where $ T^\prime \leq T $. We assign high likelihood to the full trajectories $\mathbf{x}$:
\[ p(\mathbf{x}|\{\mathbf{z}\}) \propto \prod_{i,j,l \forall i \neq j} {p(\mathbf{x}|\mathbf{z}_{ij,l})} = \text{exp}\left({-E_\theta^{ij,l}(\mathbf{x};\text{Enc}_{\theta}(\mathbf{x}(1...T^\prime))_{ij,l}}) \right),\] where $ \mathbf{z}_{ij,l} = \text{Enc}_{\theta}(\mathbf{x}(1...T^\prime))_{ij,l} $ and $ E_\theta^{ij,l} $ is the energy function linked to the $ l_\text{th} $ potential of the encoded edge between nodes $ i $ and $ j $, respectively.
Since we wish to learn a set of potentials with high likelihood for the observed trajectory $ \mathbf{x} $, as a tractable supervised manner to learn such a set of valid potentials, we directly supervise that sample using \eqn{eq:mixing} corresponds to the original trajectory $ \mathbf{x} $. In particular, we sample $ M $ steps of Langevin sampling starting from $ \tilde{\mathbf{x}}^0 $, which is initialized from uniform noise and the initial conditions fixed as the ground-truth $ \mathbf{x}(1...T_0) $: \[ \tilde{\mathbf{x}}^m = \tilde{\mathbf{x}}^{m-1}- \frac{\lambda}{2}\nabla_{\mathbf{x}}\sum_{ij,l}{E_\theta^{ij,l}(\tilde{\mathbf{x}}^{m-1};\mathbf{z}_{ij,l}} ) + \omega^m,\]
where $ m $ is the $ m_\text{th} $ step and $ \lambda $ is the step size and $ \omega^m \sim \mathcal{N}(0, \lambda) $. We then compute MSE objective with $ \tilde{\mathbf{x}}^M $, which is the result of $ M $ sampling iterations and the ground truth trajectory $ \mathbf{x} $: \[\mathcal{L}_{\text{MSE}}(\theta) = \| \tilde{\mathbf{x}}^M- \mathbf{x} \|^2.\] We optimize both $ \tilde{\mathbf{x}} $ and the parameters $ \theta $ with automatic differentiation.
Recombination
NIIP can compose relational potentials learned from two different distributions, at test-time. The process is as follows: we train two instances of our model ( $ \text{NIIP}_S $, $ \text{NIIP}_C $) to reconstruct Springs and Charged trajectories respectively. Given sample trajectories drawn from each dataset (Col. 1 for Springs and 2 for Charged), we encode them into their relational potentials. For each row, we aim to reconstruct the trajectory framed in green while swapping one of the potential pairs (green dashed box) with one drawn from the other dataset (red dashed box). As an example, in the first row of the figure, we encode the Springs trajectory with $ \text{NIIP}_S $ and the Charged trajectory with $ \text{NIIP}_C $. Next, we fix the initial conditions of the Charged trajectories and sample by optimizing the relational energy functions. To achieve recombination, each model targets specific edges. We minimize the potentials encoded by $ \text{NIIP}_S $ for the mutual edges corresponding to the nodes in green dashed boxes. The rest of edge potentials are encoded by $ \text{NIIP}_C $. The sampling process is done jointly by both models, each minimizing their corresponding potentials. The result is a natural combination of the two datasets, which affect only the targeted edges.
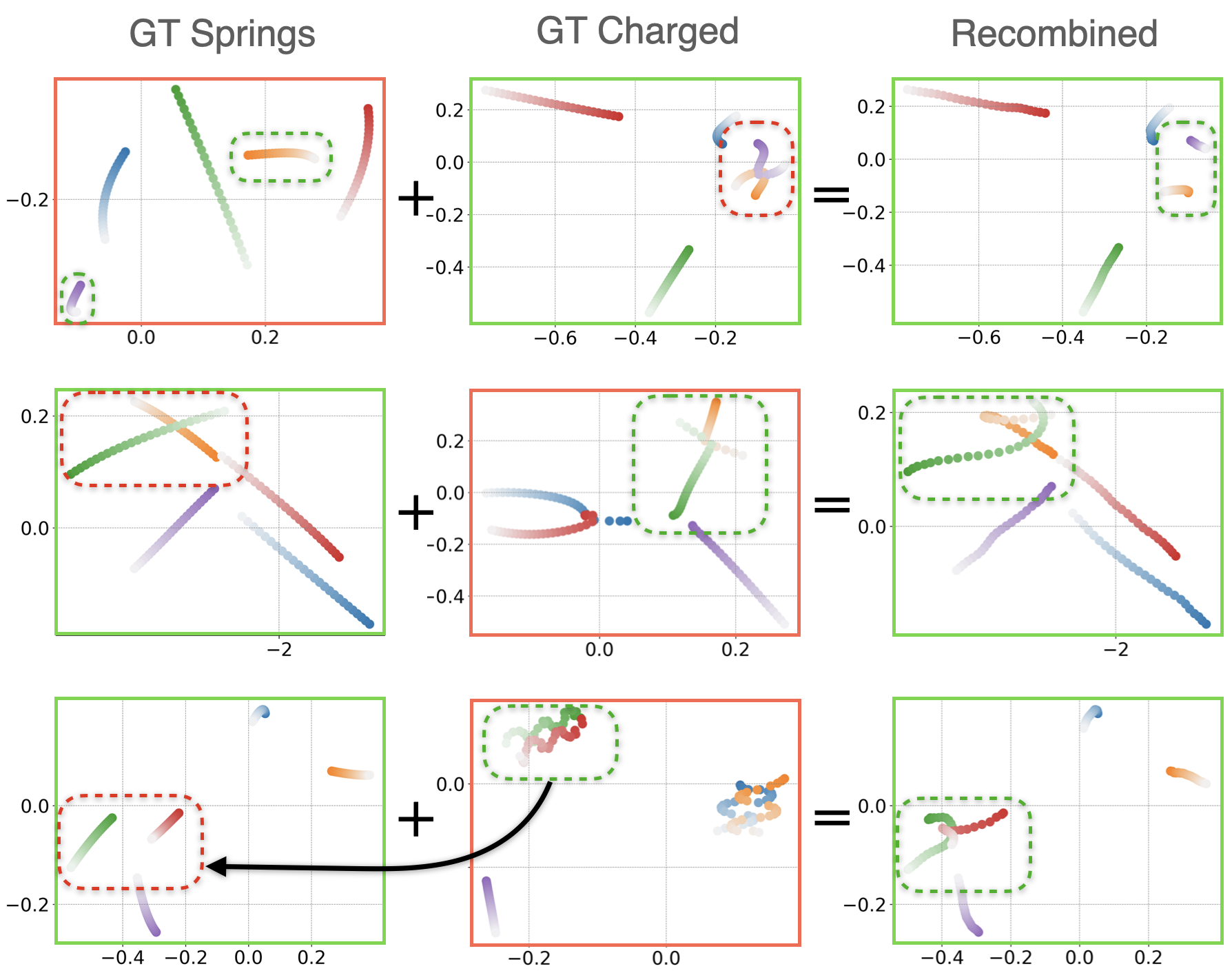
NIIP can recombine encoded potentials at test-time learned from different datasets. Illustrated, samples from Springs (Col. 1) and Charged (Col. 2) and their recombinations (Col. 3). NIIP encodes both trajectories. NIIP is able to reconstruct trajectories framed in green while swapping the edge potentials associated to the nodes in the green dashed box for the ones in the red dashed boxes. Recombinations look semantically plausible.
Out-Of-Distribution Detection
We further utilize the potential value or energy produced by NIIP over a trajectory to detect out-of-distribution interactions in a trajectory. In our proposed architecture, energy is evaluated at the node level. Therefore, if NIIP has been trained with a specific dataset, the potentials associated to out-of-distribution type of edges are expected to correspond to higher energy. We design a new dataset (Charged-Springs) as a combination of Springs and Charged interaction types. The figure below shows qualitatively how the energy is considerably higher for the nodes with Charged-type forces (drawn in red) when trained for Springs. Quantitative results are summarized in the Table below for 1k test samples.

(Left, Figure) Out-Of-Distribution Detection with NIIP. A model trained with certain relation types can detect when a trajectory exhibits a new type of relation. The illustrated trajectories show the energy associated to each one of the nodes. (Right, Table) Quantitative evaluation of out-of-distribution detection. We evaluate the average energy associated to each node-type in a scene.
Flexible Generation
Another advantage of our approach is that it can flexibly incorporate test-time user specified potentials. For this experiment, we investigate three different sets of potentials.
Avoid Area Potentials In this case, we penalize the portion of the predicted trajectory $ \tilde{\mathbf{p}}^{t}_i $ that is inside a given restricted area $ \mathbf{A} $. We do so by computing the distance of each particle $ i $ that lays within the region $ \mathbf{A} $ to the borders $ \mathbf{b}_A $ of $ \mathbf{A} $. The added potential is: $ P = \epsilon\lambda \sum_{i,t}(\tilde{\mathbf{p}}_{A,i}^{0:T-1} - \mathbf{b}_A - C)^2 $, where $ C $ is a small margin that ensures that the particles are repelled outside of the boundaries of $ \mathbf{A} $. With $ \lambda =1e-3/{N} $. In the Table below (row 2), we explore the effect of different strengths of this potential type, in the prediction task. We also provide a visual example. For this experiment, we avoid the area $ \mathbf{A} = [(0, -1), (1, 1)] $, which corresponds to half of the box (see Figure). We use the following parameters: (i.) $ s1: \epsilon=1 $, (ii.) $ s2: \epsilon=5e1 $ and (iii.) $ s3: \epsilon=5e2 $ .
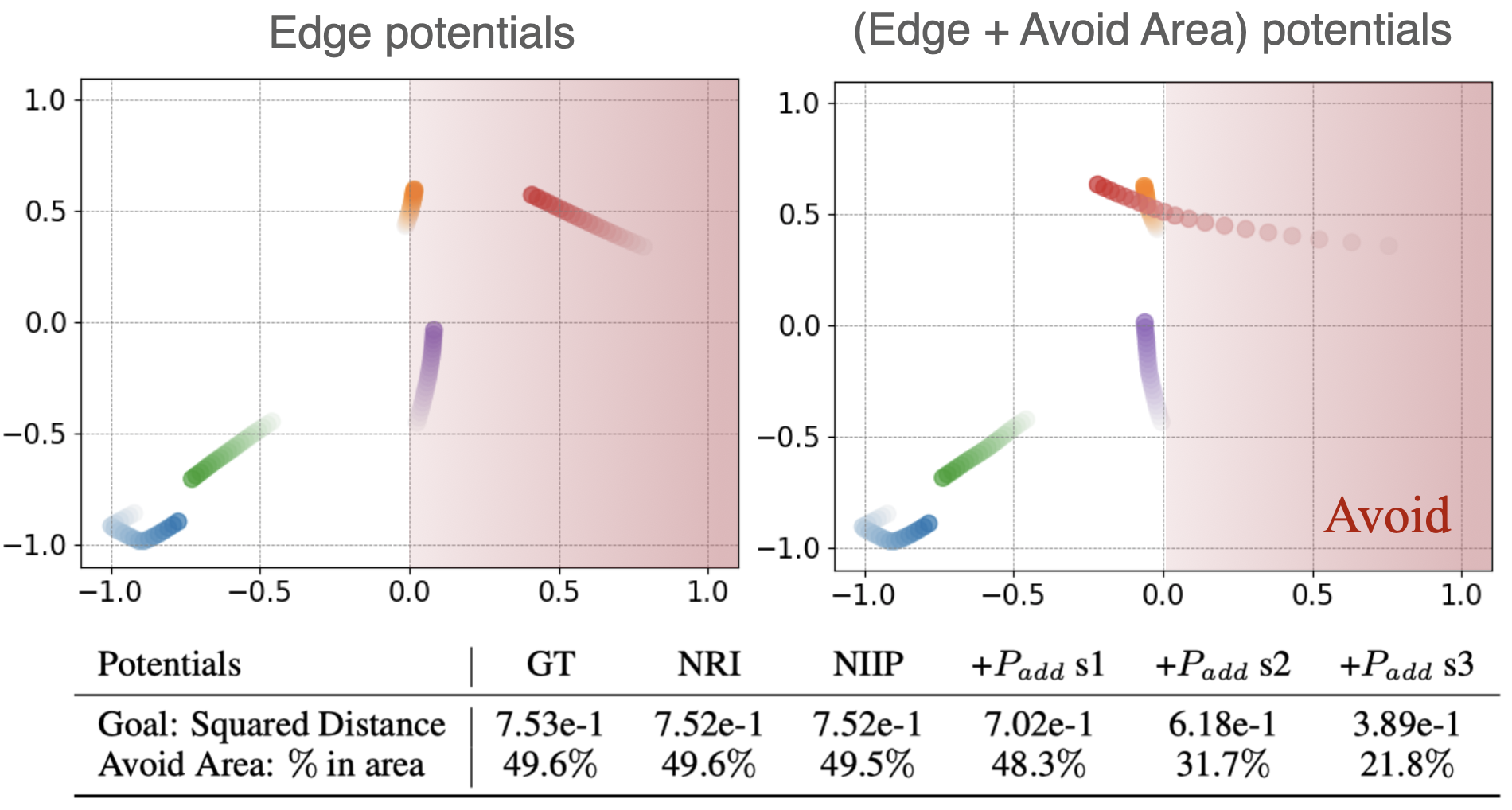
(Top, Figure) With NIIP we can add and control test-time potentials to achieve a desired behavior for Prediction in the Charged Dataset. We design test-time potentials to steer trajectories out of a prohibited area. (Bottom, Table) Quantitative results.. In row 1 of the table, we show the squared distance after applying a goal potential towards the center (0,0) of the scene with different strengths. In row 2, we report the percentage of time-steps that particles stay in a particular area A = [(0, −1), (1, 1)] after applying a potential that enforces avoiding A. The figure shows the effect of applying test-time potentials in the latter experiment.
Velocity Potentials. We incorporate the following velocity potential as an energy function: $ E = \epsilon \lambda \sum_{i,t}\sqrt{(\mathbf{v}_{x,i}^t)^2 + (\mathbf{v}_{y,i}^t)^2}$, for particle $ i $ in time $ t $. The weight $ \lambda =1e-2/{N} $ scales the effect of this function over the rest and $ \epsilon $ is a multiplicative constant that indicates the strength and direction of the potential.
Goal Potentials. We also add at test-time an attraction potential as a the squared distance of the predicted coordinates to the goal: $ P = \epsilon\lambda \sum_{i,t}(\tilde{\mathbf{p}}^{0:T-1}_i - \mathbf{g})^2 $, where $ \mathbf{g} $ is defined as the coordinates of our goal point. We define the trajectory coordinates $ \tilde{\mathbf{p}}^{t}_i $ as an accumulation of the un-normalized velocities $ \mathbf{v}^{t}_i $ predicted by NIIP: $ \tilde{\mathbf{p}}^{t+1}_i = \sum_{t}(\mathbf{v}^{0:t}_i) + \mathbf{p}^0_i $ for particle $ i $ at time-step $ t $. Here, $ \mathbf{p}^1 $ is fixed initial ground-truth location of the particle at time 0 and $ \lambda =5e-4/{N}$.
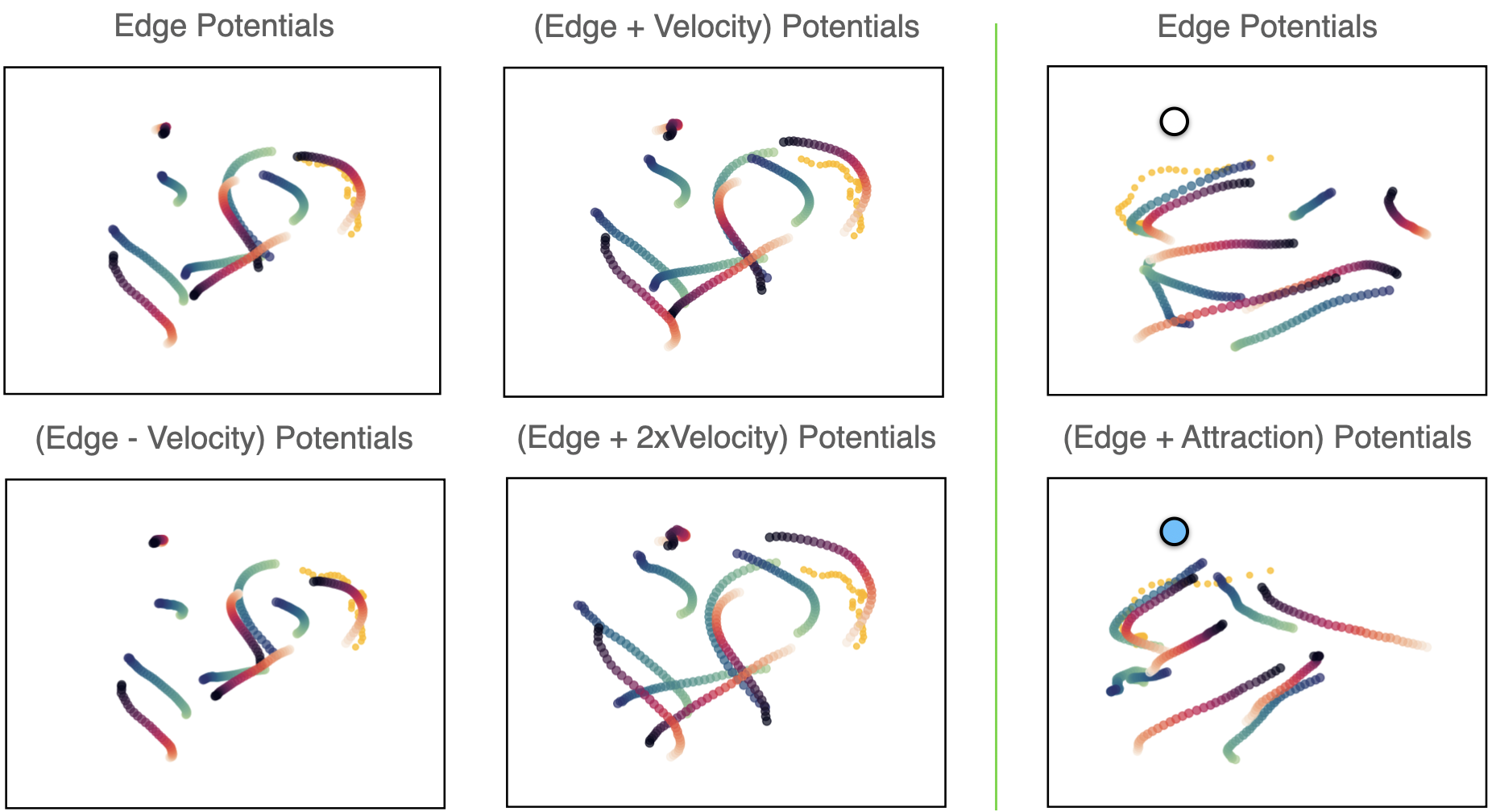
NIIP is able to incorporate new potentials in test-time. We can see depicted reconstructions of NBA samples with added potentials. Trajectories are appropriately modified according to each added potential.
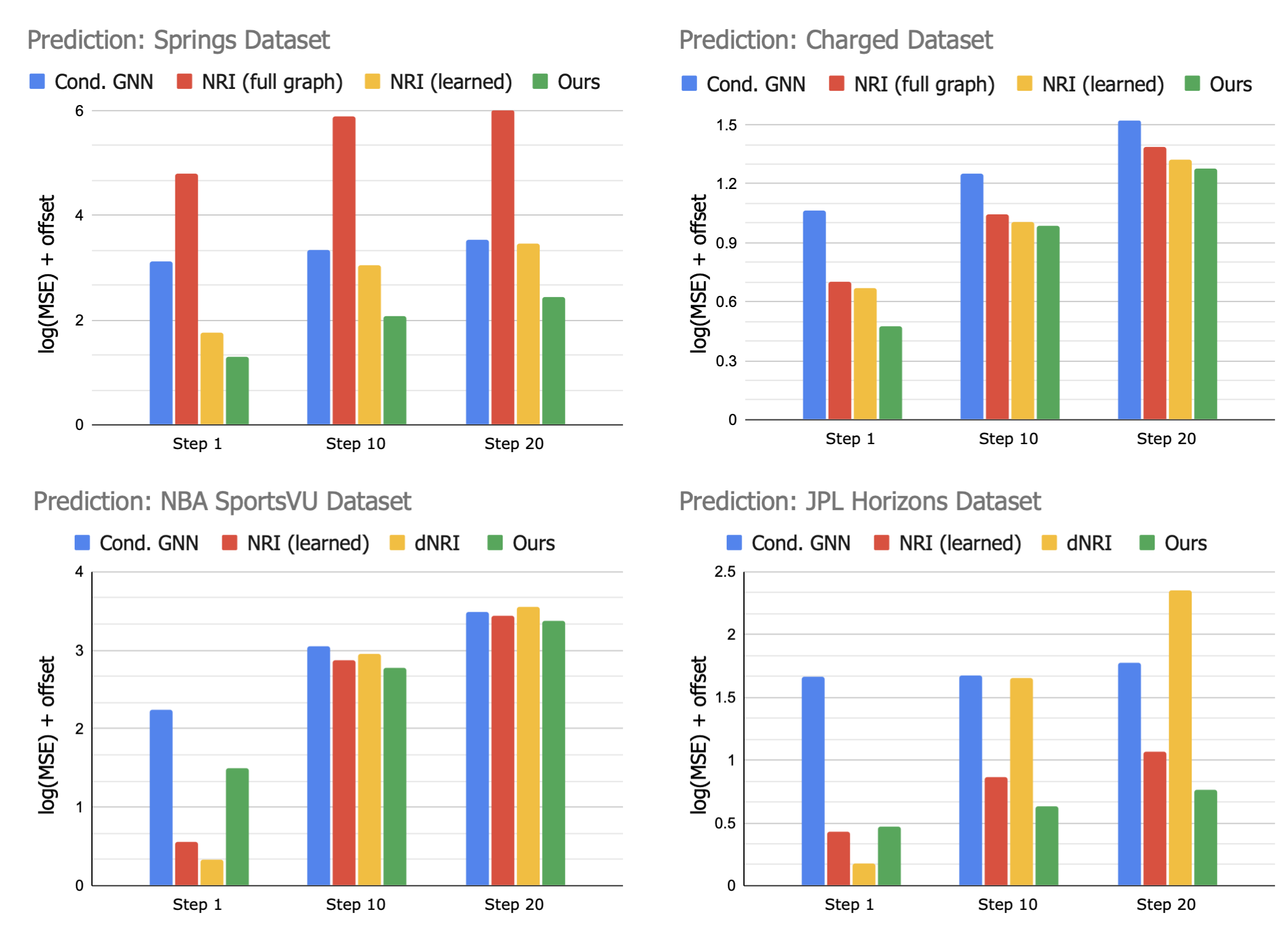
Forecasting
We asses NIIP's capabilities for trajectory forecasting. NIIP can predict trajectories faithfully in the future, displaying favorable mid- and long-term performance when compared to existing approaches.