Reduce, Reuse, Recycle: Compositional Generation with Energy-Based Diffusion Models and MCMC
Abstract
Since their introduction, diffusion models have quickly become the prevailing approach to generative modeling in many domains. They can be interpreted as learning the gradients of a time-varying sequence of log-probability density functions. This interpretation has motivated classifier-based and classifier-free guidance as methods for post-hoc control of diffusion models. In this work, we build upon these ideas using the score-based interpretation of diffusion models, and explore alternative ways to condition, modify, and reuse diffusion models for tasks involving compositional generation and guidance. In particular, we investigate why certain types of composition fail using current techniques and present a number of solutions. We conclude that the sampler (not the model) is responsible for this failure and propose new samplers, inspired by MCMC, which enable successful compositional generation. Further, we propose an energy-based parameterization of diffusion models which enables the use of new compositional operators and more sophisticated, Metropolis-corrected samplers. Intriguingly we find these samplers lead to notable improvements in compositional generation across a wide variety of problems such as classifier-guided ImageNet modeling and compositional text-to-image generation.
Method
Existing diffusion models are often trained on massive datasets with a vast amounts of computational resources. In this paper, we explore and present tools on how we may utilize probabilistic composition of as an algebra to repurpose diffusion models, without any finetuning, for variety of downstream tasks.
Consider two probability distributions $q^1(x)$ and $q^2(x)$, each represented with a different diffusion model. Can we draw samples from the product distribution $q^{\textup{prod}}(x) \propto q^1(x)q^2(x)$ specified by each diffusion model? One potential solution is to note that the diffusion process encodes the noisy gradients of each distribution, letting us use the sum of the scores of each diffusion process to compose these models. While this approach can be effective, it is not completely mathematically accurate. To correctly sample from a reverse diffusion corresponding to $q^{\textup{prod}}(x)$, at each noise timestep $t$, we must compute the score:
\[ \nabla_{x}\log \tilde{q}_{t}^{\textup{ prod}}(x_t) = \nabla_x\log \left(\int
dx_{0}
q^{1}(x_{0})q^2(x_{0})~ q(x_t|x_{0})\right).\]
Directly summing up the predicted scores of each separate diffusion model instead gives us the score:
\[ \nabla_{x}\log q_{t}^{\textup{prod}}(x_t)
=
\nabla_{x}\log \left(\int dx_0 q^1(x_0)q(x_t|x_0)\right)+\nabla_{x}\log \left(\int dx_0 q^2(x_0)q(x_t|x_0)\right).\]
When the $t > 0$, the above expressions are not equal, and thus sample from the incorrect reverse diffusion process for $q^{\textup{prod}}(x)$. To address this theoretical issue, we propose two methodological contributions to properly sample across a set of different compositions of diffusion models (see our paper for analysis of why other forms of composition fail):
Sampling from Composed Diffusion Models using Annealed MCMC: While the score estimate $\nabla_{x}\log q_{t}^{\textup{prod}}(x_t)$ does not correspond to the correct score estimate necessary to sample from the reverse diffusion process for $q_{t}^{\textup{prod}}(x_t)$, it does define a unnormalized probability distribution (EBM) at timestep t. The sequence of score estimates across different time points can then be seen as defining an annealed sequence of distributions starting from Gaussian noise and evolving to our desired distribution $q_{t}^{\textup{prod}}(x_t)$. Thus, we may still sample from $q_{t}^{\textup{prod}}(x_t)$ using Annealed MCMC procedure, where we initialize a sample from Gaussian noise, and draw samples sequentially across different intermediate distributions by running multiple steps of MCMC sampling initialized from samples from the previous distribution.
Energy Based Diffusion Parameterization: In practice, MCMC sampling does not correctly sample from underlying distribution without a Metropolis Adjustment step. With the typical score parameterization of diffusion models, this is not possible, as there is no unnormalized density associated with the score field. Instead, we propose to use an energy based parameterization of diffusion model, where at each timestep, our neural network predicts an scalar energy value for each data point and the utilizes the gradient of the energy with respect to the input as the score for the diffusion process. The predicted energy gives us an unnormalized estimate of the probability density, enabling us to use Metropolis Adjustment in sampling. We further show that the unnormalized estimate of the density enables us to do additional compositions with a diffusion model.
Below, we demonstrate results illustrating how we may use the above tools to re-purpose diffusion models in a variety of different settings.
2D Distribution Composition
First, we illustrate how we may generate samples from compositions of two 2D distributions $p_1(x)$ and $p_2(x)$, each represented using a seperately trained diffusion model. Here, we illustrate two compositions, the product and mixture of the two distributions (see the paper for more examples). To enable the mixture of two distributions, we must use our energy-based diffusion parameterization, as we need a unnormalized density estimate of the probability of the sample under each model.
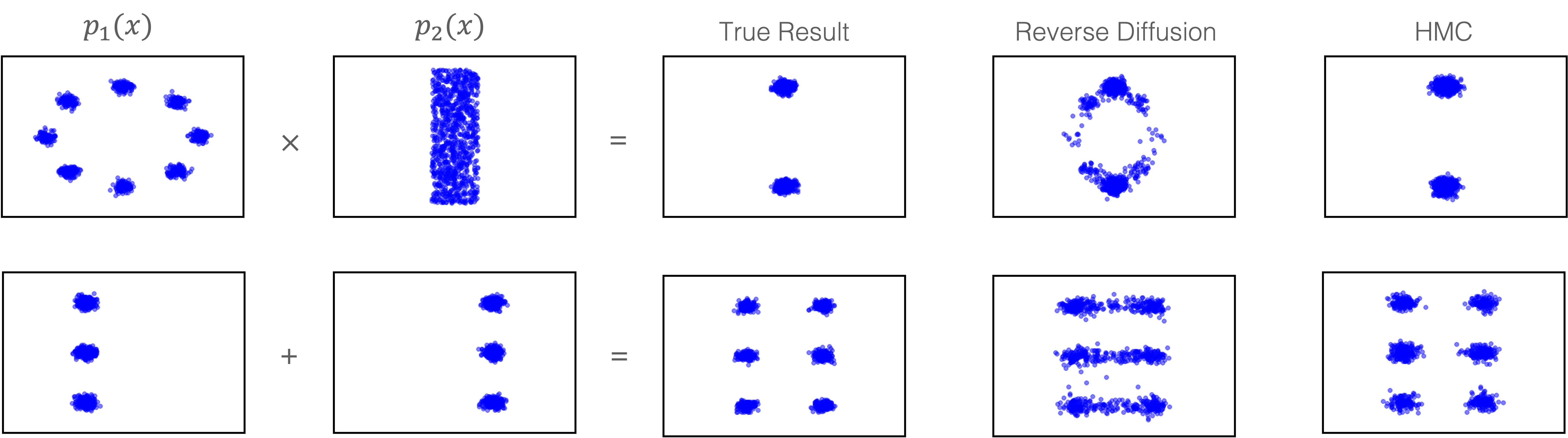
Our proposed techniques enable us to take two separately trained diffusion models on distributions $p_1(x)$ and $p_2(x)$ and generate samples from various compositions of these distributions.
Object Generation
We may repurpose a diffusion model which generates an object at a single position $y_i$ to generate multi-object scenes with $c$ objects by utilizing the following probability decomposition: \[ \log p_\theta(x | y_1, \ldots, y_c) = \log p_\theta(x) + \sum_{i=1}^c \left( \log p_\theta(x | y_i) - \log p_\theta(x) \right). \] Below, we illustrate the results when using this decomposition. Our probabilistic repurposing enables us to accurately generate 5 different cubes in a scene. The use of MCMC sampling to transition between annealed distributions substantially improves the ability to generate multi-object scenes, with increasing number of steps of MCMC improving the underlying compositional generation performance (right image).
a) Using a HMC sampling procedure enables more accurate generation of multi-object scenes. b) The accuracy of sampling from composed distribution monotonically increases with the number of MCMC sets with Metropolis Adjustment (enabled by a energy-based diffusion parameterization) significantly improving compositional performance.
Class-Conditional Generation
We may repurpose an unconditional diffusion for conditional image generation by utilizing the probability distribution corresponding to the gradient estimate: \[ \nabla_x\log p_\theta(x | y, t) = \nabla_x\log p_\theta(x | t) + \nabla_x\log p_\theta(y | x, t). \] To sample from this distribution, in classifer based guidance, this gradient estimate is directly plugged into the reverse diffusion procedure. Below, we illustrate that conditional image sampling can be substantially improved by using HMC to effectively transition between annealed distributions.

HMC sampling transitions enables more accurate classifier based generation of images
Compositional Text-to-Image Generation
We may also probabilistically repurpose a text-to-image model for compositional image generation. For example, given a complex scene description: \[ \text{``A horse'' \texttt{AND} (``A sandy beach'' \texttt{OR} ``Grass plains'') \texttt{AND} (\texttt{NOT} ``Sunny'').} \] We may utilize probability as an algebra to specify this complex scene description: \[ p^{\text{comp}}_\theta(x|y_{\text{text}}) \propto \frac{p_\theta(x|\text{``A horse''})\left[\frac{1}{2}p_\theta(x|\text{``A sandy beach''}) + \frac{1}{2}p_\theta(x|\text{``Grass plains''})\right]}{p_\theta(x|\text{``Sunny''})^\alpha}. \] We may then sample from this composed distribution consisting of multiple instances of the text-to-image model using the sampling procedures described above. We provide example illustrations of this procedure below:

By composing different energy-based text-to-image diffusion models we can generate complex combinations of natural language descriptions.
Image Tapestries
While text-to-image models generate images given natural language prompts, it is difficult to control the spatial location of different content, and difficult to generate images at higher resolutions than used during training. We may further compose multiple overlapping text-to-image models, at a variety of scales, to construct an image tapestry with different specified content at different locations and scales.









