Potential Based Diffusion Motion Planning and Generalization. Our method encodes motion planning constraints to latent vectors and uses the potential functions to generate motion plans. We show that our method can directly generalize to cluttered heterogeneous environments via composing potentials, while the potential functions are only trained on simple homogeneous environments.
Effective motion planning in high dimensional spaces is a long-standing open problem in robotics. One class of traditional motion planning algorithms corresponds to potential-based motion planning. An advantage of potential based motion planning is composability -- different motion constraints can be easily combined by adding corresponding potentials. However, constructing motion paths from potentials requires solving a global optimization across configuration space potential landscape, which is often prone to local minima. We propose a new approach towards learning potential based motion planning, where we train a neural network to capture and learn an easily optimizable potentials over motion planning trajectories. We illustrate the effectiveness of such approach, significantly outperforming both classical and recent learned motion planning approaches and avoiding issues with local minima. We further illustrate its inherent composability, enabling us to generalize to a multitude of different motion constraints.
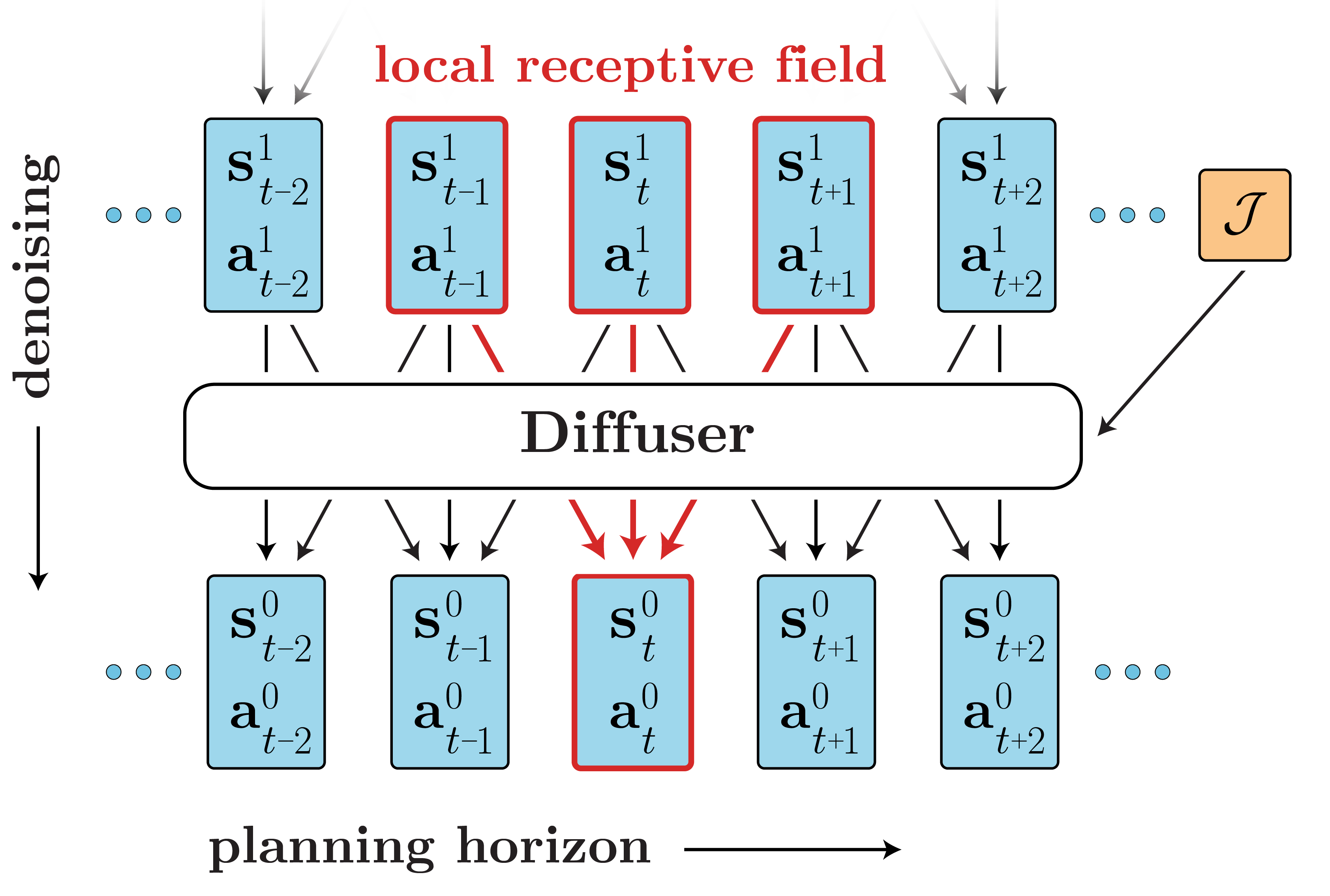
Trajectory Denoising Process on Maze2D. Motion trajectories are randomly initialized from Gaussian distribution in timestep $S = 100$. Noises are iteratively removed via the gradient of the energy function. A feasible collision-free trajectory can be obtained at timestep $S = 0$. We use DDIM to accelerate sampling speed.
Maze2D 6+6 Obstacles

Our method can generalize to more difficult out-of-distribution environments by sampling from the composite diffusion potential function. We demonstrate qualitative results where we compose potentials of the same obstacle type, of different obstacle types, and of static and dynamic obstacles. Please see our paper for more comprehensive results.
@inproceedings{
luo2024potential,
title={Potential Based Diffusion Motion Planning},
author={Yunhao Luo and Chen Sun and Joshua B. Tenenbaum and Yilun Du},
booktitle={Forty-first International Conference on Machine Learning},
url={https://openreview.net/forum?id=Qb68Rs0p9f}
year={2024},
}